Mengapa hasil kali Gradien 2 garis yang saling tegak lurus adalah -1?
Dalam postingan ini saya akan menjawab pertanyaan diatas.

Diberikan 2 garis 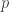 dan
dan 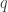 yang saling tegak lurus. Tanpa mengurangi generalitas (Without loss of generality) diasumsikan kedua garis berpotongan dititik awal
yang saling tegak lurus. Tanpa mengurangi generalitas (Without loss of generality) diasumsikan kedua garis berpotongan dititik awal  . Karena sebenarnya kedua garis dapat digeser kemana saja tanpa merubah gradient. Andaikan terdapat titik
. Karena sebenarnya kedua garis dapat digeser kemana saja tanpa merubah gradient. Andaikan terdapat titik  pada garis
pada garis 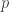 dan titik
dan titik  pada garis
pada garis 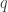 , seperti ditunjukan pada gambar diatas. Diperoleh gradien garis
, seperti ditunjukan pada gambar diatas. Diperoleh gradien garis 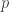 adalah
adalah  dan gradien garis
dan gradien garis 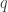 adalah
adalah  .
.
Kita akan membuktikan 
Ketiga titik  ,
,  dan
dan 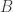 membentuk segitiga siku-siku dengan sudut siku-siku pada sudut
membentuk segitiga siku-siku dengan sudut siku-siku pada sudut  .
.
Gunakan teorema Pythagoras, diperoeleh
(jarak  ke
ke  )²+ (jarak
)²+ (jarak  ke
ke 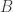 )²=(jarak
)²=(jarak  ke
ke 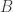 )²
)²
Silahkan kalian jabarkan sendiri, diperoleh
Dari persamaan terakhir dengan mudah diperoleh
Terbukti hasil kali Gradien 2 garis yang saling tegak lurus adalah -1


0 komentar:
Posting Komentar